机器学习(五):通俗易懂决策树与随机森林及代码实践
2021-02-25
与SVM一样,决策树是通用的机器学习算法。随机森林,顾名思义,将决策树分类器集成到一起就形成了更强大的机器学习算法。它们都是很基础但很强大的机器学习工具,虽然我们现在有更先进的算法工具来训练模型,但决策树与随机森林因其简单灵活依然广受喜爱,建议大家学习。
一、决策树
1.1 什么是决策树
我们可以把决策树想象成IF/ELSE判别式深度嵌套的二叉树形结构。以我们在《机器学习(三):理解逻辑回归及二分类、多分类代码实践》所举的鸢尾花数据集为例。
我们曾用seaborn绘制花瓣长度和宽度特征对应鸢尾花种类的散点图,如下:
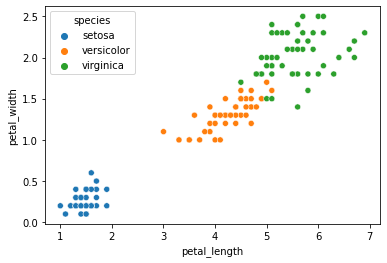
当花瓣长度小于2.45则为山鸢尾(setosa),剩下的我们判断花瓣宽度小于1.75则为变色鸢尾(versicolor)剩下的为维吉尼亚鸢尾(virginica)。那么我用导图画一下这种判别式的树形结构如下:
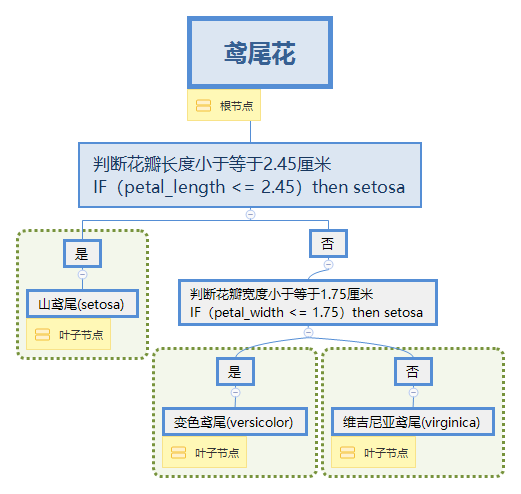
因此,当我们面对任意鸢尾花的样本,我们只需要从根节点到叶子节点遍历决策树,就可以得到鸢尾花的分类结论。
这就是决策树。
1.2 决策树代码实践
我们导入数据集(大家不用在意这个域名),并训练模型:
我们来可视化决策树:

如上图,我们可以看到根节点总实例数为150时,由value = [50, 50, 50]可知,实际样本分类为50个山鸢尾花实例、50个变色鸢尾花实例、50个维吉尼亚鸢尾花实例。我们再看最末尾右侧的叶子节点(紫色),由value = [0, 1, 45]可知,实际样本分类为0个山鸢尾花实例、1个变色鸢尾花实例、45个维吉尼亚鸢尾花实例。
那么gini = 0.043是什么意思呢?
1.3 基尼不纯度
显然我们进行分类时,每一个类别实际混入其他类的数量越少分类就越纯粹,这种纯度我们通过如下公式表示:
$$ G_i = 1 - \sum_{k=1}^{n}{p^2_{i,k}} $$
我们计算维吉尼亚鸢尾花节点(紫色)的gini系数1-((0/46)**2 + (1/46)**2 + (45/46)**2) = 0.04253308128544431 ≈0.043 。
我们使用基尼(gini)不纯度来衡量决策树的好坏。那么我们通过最小化基尼不纯度min(gini)来求解X[0],X[1](即,花瓣长度宽度特征)边界的过程就决策树模型的训练过程。
二、随机森林
2.1 大数定理与随机森林
其实随机森林很简单,我们把决策树随机组合在一起就是随机森林,它比单个的决策树更有效。
凭什么?
假设我们有一枚不均匀的硬币,投掷它有51%的概率为正面,49%的概率为背面,那么当投掷1000次时,“大多数为正面"这件事的概率为75%。投掷10000次时,“大多数为正面"这件事的概率为97%。这就是大数定理,它体现的是群体智慧。质量不够,数量来凑。由此可知,当前寻找最佳模型的方法不止是技巧的比拼,也同样是算力的比拼。
2.2 随机森林代码实践
2.2.1. 引入新的数据集
添加引用:
导入数据集(大家不用在意这个域名):
| species | island | culmen_length_mm | culmen_depth_mm | flipper_length_mm | body_mass_g | sex |
|---|---|---|---|---|---|---|
| Adelie | Torgersen | 39.1 | 18.7 | 181 | 3750 | MALE |
| Adelie | Torgersen | 39.5 | 17.4 | 186 | 3800 | FEMALE |
| Adelie | Torgersen | 40.3 | 18 | 195 | 3250 | FEMALE |
| Adelie | Torgersen | 36.7 | 19.3 | 193 | 3450 | FEMALE |
| Adelie | Torgersen | 39.3 | 20.6 | 190 | 3650 | MALE |
企鹅数据集包含特征和标签如下:
- 特征:所在岛屿island、鸟喙长度culmen_length_mm、鸟喙深度culmen_depth_mm、脚蹼长度flipper_length_mm、体重(g)、性别
- 标签:物种species:Chinstrap, Adélie, or Gentoo
2.2.2 观察数据
我们通过pairplot方法绘制特征两两之间的对应关系。
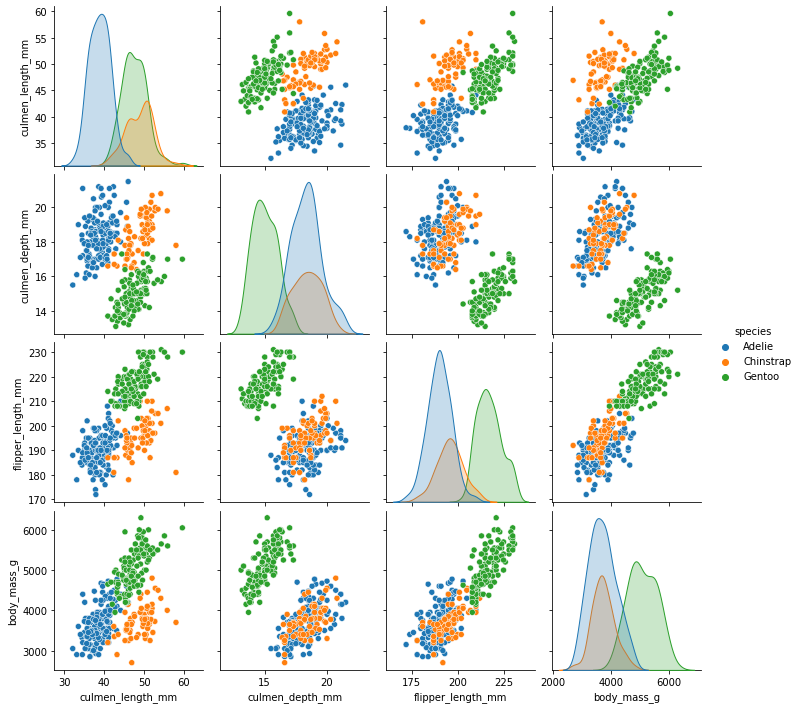
2.2.3 预处理
注意,get_dummies方法将字符串属性的列转换成了数字属性的多个列。如,岛屿island和性别sex分别转换成了island_Dream、island_Torgersen和sex_FEMALE、sex_MALE。这是一种独热编码的关系,比如sex_FEMALE与sex_MALE属性独立,在空间内没有向量关系。
| culmen_length_mm | culmen_depth_mm | flipper_length_mm | body_mass_g | island_Dream | island_Torgersen | sex_FEMALE | sex_MALE |
|---|---|---|---|---|---|---|---|
| 39.1 | 18.7 | 181 | 3750 | 0 | 1 | 0 | 1 |
| 39.5 | 17.4 | 186 | 3800 | 0 | 1 | 1 | 0 |
| 40.3 | 18 | 195 | 3250 | 0 | 1 | 1 | 0 |
| 36.7 | 19.3 | 193 | 3450 | 0 | 1 | 1 | 0 |
| 39.3 | 20.6 | 190 | 3650 | 0 | 1 | 0 | 1 |
2.2.4 训练数据
使用随机森林分类器RandomForestClassifier训练,得到模型精度为97%。
2.2.5 网格搜索与AdaBoost提升法(拓展)
我们使用AdaBoostClassifier分类器集成数个决策树分类器DecisionTreeClassifier进行分类。并使用网格搜索方法GridSearchCV来寻找最优参数。
这是一种集成学习技术,输出如下:
grid.best_params_ = {'algorithm': 'SAMME', 'learning_rate': 1, 'n_estimators': 20} , grid.best_score_ = 0.9914893617021276
总结
二叉树是决策树的核心逻辑,随机森林是大数定理的应用实现。这种基本思想即使不用数学公式也可以很容易的解释清楚,这也是我做这个系列课程(文章)的主要风格特点。我认为,数学是对现实世界的解释,但现实世界并不能被数学完全解释。像谷歌AI主管Laurence Moroney所说:
很多人害怕数学,害怕大量的深度的微积分知识。其实我们可以实现编码而不考虑数学,我们可以使用TensorFlow中高(层)级的API,来解决问题,如自然语言处理,图像分类,计算机视觉序列模型等而无需理解深刻的数学。就像你使用JAVA却不一定非要掌握它是如何编译的。未来,AI只是每个开发者技术栈(toolbox)中的一部分,就像HTML, CSS, JAVA。
希望那一天可以早点到来吧……
往期文章: